Công thức tính diện tích hình thang, cách tính diện tích hình thang: vuông, cân, khi biết độ dài 4 cạnh
Hình thang là hình gặp khá nhiều trong cuộc sống hằng ngày, khi học các chương trình học THCS PTTH bạn cũng có thể gặp nhiều bài tập liên quan tới hình thang. Nếu như việc tính chu vi hình thang thì khá dễ nhớ bằng tổng 4 cạnh thì công thức tính diện tích hình tháng lâu ngày có thể bạn sẽ khó nhớ. Các bạn có thể tham khảo công thức tính các hình thang thường, vuông hoặc biết 4 cạnh bằng các công
1. Công thức tính diện tích hình thang
Trước tiên tính công thức chung của hình thang chúng ta sẽ có công thức: trung bình cộng 2 cạnh đáy nhân với chiều cao giữa 2 đáy
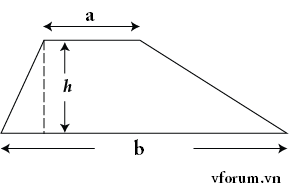
Trong đó
a: Cạnh đáy 1
b: cạnh đáy 2
h: Chiều cao hạ từ cạnh đấy a xuống b hoặc ngược lại(khoảng cách giữa 2 cạnh đáy)
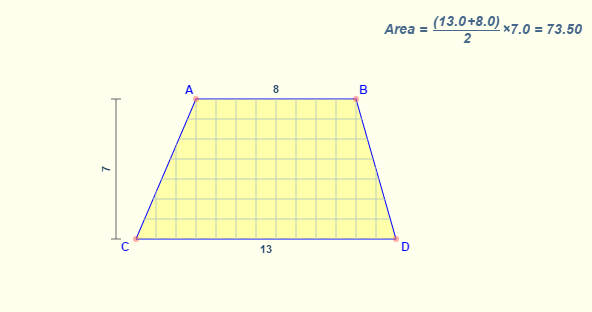
Ví dụ cụ thể giả sử ta có hình thang ABCD với các cạnh AB = 8, cạnh đáy CD = 13, chiều cao giữa 2 cạnh đáy là 7 thì chúng ta sẽ có diện tích hình thang là:
S(ABCD) = (8+13)/2 * 7 = 73.5
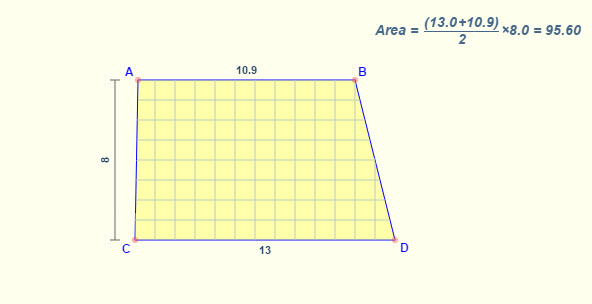
Tương tự ví dụ với trường hợp hình thang vuông chúng ta cũng tính tương tự
S(ABCD) = (AB + CD)/2 * AC = (10.9 + 13)/2 * 8 = 95.6
2. Tính diện tích hình thang khi biết 4 cạnh
Thực tế nếu bài toán đưa ra câu hỏi cách tính 4 cạnh của hình thang khi biết 4 cạnh thì sẽ không có đáp án chính xác vì chỉ biết 4 cạnh thì có rất nhiều trường hợp xay ra và diện tích cũng khác nhau, các bạn có thể hình dung ví dụ hình thang dưới đây có 4 cạnh 4 5 6 9 có thể vẽ 3 dạng hình khác nhau với diện tích khác nhau
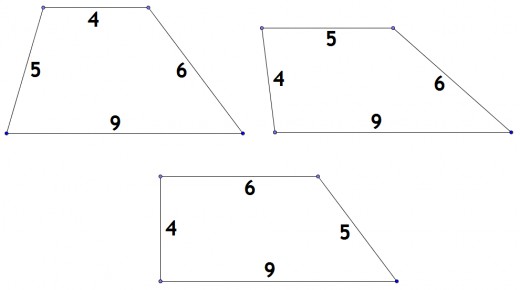
Tuy nhiên nếu bài toán cho thêm vài dữ kiện ví dụ như tính diện tích hình thang khi biết độ dài 4 cạnh và có nõi rõ cạnh đáy là cạnh nào thì có thể tính được diện tích hình thang, ví dụ chúng tao có các cạnh đấy Q P, trong đó cnahj đáy P dài hơn và 2 cạnh bên R và S
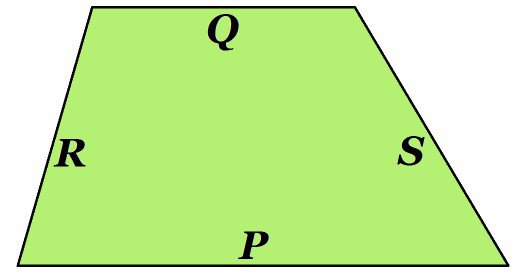
Thì có thể áp dụng công thức tính diện tích hình thang như sau
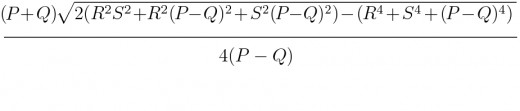
Ngoài ra trong trường hợp tính diện tích hình thang khi biết các cạnh các bạn có thể tách ra thành 2 tam giác và 1 hính chữ nhật hoặc kẻ thêm đường giao giữa 2 cạnh bên và áp dụng công thức Herong tính diện tích tam giác và suy ra được diện tích hình thang. Công thức trên cũng được hình thành từ cách này
Hình thang là hình gặp khá nhiều trong cuộc sống hằng ngày, khi học các chương trình học THCS PTTH bạn cũng có thể gặp nhiều bài tập liên quan tới hình thang. Nếu như việc tính chu vi hình thang thì khá dễ nhớ bằng tổng 4 cạnh thì công thức tính diện tích hình tháng lâu ngày có thể bạn sẽ khó nhớ. Các bạn có thể tham khảo công thức tính các hình thang thường, vuông hoặc biết 4 cạnh bằng các công
1. Công thức tính diện tích hình thang
Trước tiên tính công thức chung của hình thang chúng ta sẽ có công thức: trung bình cộng 2 cạnh đáy nhân với chiều cao giữa 2 đáy

S = 1/2(a+b) * h
Trong đó
a: Cạnh đáy 1
b: cạnh đáy 2
h: Chiều cao hạ từ cạnh đấy a xuống b hoặc ngược lại(khoảng cách giữa 2 cạnh đáy)
Ví dụ cụ thể giả sử ta có hình thang ABCD với các cạnh AB = 8, cạnh đáy CD = 13, chiều cao giữa 2 cạnh đáy là 7 thì chúng ta sẽ có diện tích hình thang là:
S(ABCD) = (8+13)/2 * 7 = 73.5

Tương tự ví dụ với trường hợp hình thang vuông chúng ta cũng tính tương tự
S(ABCD) = (AB + CD)/2 * AC = (10.9 + 13)/2 * 8 = 95.6

2. Tính diện tích hình thang khi biết 4 cạnh
Thực tế nếu bài toán đưa ra câu hỏi cách tính 4 cạnh của hình thang khi biết 4 cạnh thì sẽ không có đáp án chính xác vì chỉ biết 4 cạnh thì có rất nhiều trường hợp xay ra và diện tích cũng khác nhau, các bạn có thể hình dung ví dụ hình thang dưới đây có 4 cạnh 4 5 6 9 có thể vẽ 3 dạng hình khác nhau với diện tích khác nhau

Tuy nhiên nếu bài toán cho thêm vài dữ kiện ví dụ như tính diện tích hình thang khi biết độ dài 4 cạnh và có nõi rõ cạnh đáy là cạnh nào thì có thể tính được diện tích hình thang, ví dụ chúng tao có các cạnh đấy Q P, trong đó cnahj đáy P dài hơn và 2 cạnh bên R và S

Thì có thể áp dụng công thức tính diện tích hình thang như sau
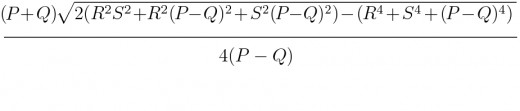
Ngoài ra trong trường hợp tính diện tích hình thang khi biết các cạnh các bạn có thể tách ra thành 2 tam giác và 1 hính chữ nhật hoặc kẻ thêm đường giao giữa 2 cạnh bên và áp dụng công thức Herong tính diện tích tam giác và suy ra được diện tích hình thang. Công thức trên cũng được hình thành từ cách này
Sửa lần cuối bởi điều hành viên: